蒙特卡羅模擬（Monte Carlo Simulation）

蒙特卡羅模擬（Monte Carlo Simulation）是一種基於隨機抽樣的計算方法，用於模擬和分析複雜系統或過程中的不確定性。它通過多次隨機試驗來估計結果的概率分布，廣泛應用於金融、工程、物理、統計等領域。

核心概念

1. 隨機抽樣：模擬中會從定義的概率分布中隨機抽取變量值，模擬可能的輸入情景。
2. 多次試驗：通過重複執行大量試驗（通常數千到數百萬次），生成大量可能的結果。
3. 統計分析：根據試驗結果，計算期望值、概率分布或其他統計指標，來評估系統行為或風險。

工作原理

• 步驟：

1. 定義問題和模型：確定需要模擬的系統，明確輸入變量（如成本、時間、利率等）及其概率分布。
2. 生成隨機輸入：根據變量的概率分布（如常態分布、均勻分布等），隨機生成輸入值。
3. 計算結果：將隨機輸入代入模型，計算每次試驗的輸出。
4. 重複試驗：進行大量試驗，收集每次的結果。
5. 分析結果：對所有試驗結果進行統計分析，得出概率分布、平均值、風險等。

應用範例

1. 金融：評估投資組合風險、預測股價波動或定價衍生品（如期權）。
2. 工程：分析結構可靠性和故障概率。
3. 項目管理：估計項目完成時間或成本，考慮不確定因素。
4. 物理：模擬粒子運動或量子系統行為。

簡單例子

假設你想估計一個項目的完成時間，假設有三個任務，每個任務的完成時間服從某個概率分布：

• 任務A：5至7天（均勻分布）
• 任務B：3至5天（均勻分布）
• 任務C：2至4天（均勻分布）

蒙特卡羅模擬會：

1. 隨機抽取每個任務的完成時間（例如：A=6天，B=4天，C=3天）。
2. 計算總時間（6+4+3=13天）。
3. 重複此過程數千次，記錄每次的總時間。
4. 分析結果，得出總時間的概率分布（如90%的概率在12至15天內完成）。

優點

• 能處理高度不確定性和複雜的非線性問題。
• 提供結果的概率分布，而不僅僅是單一預測值。
• 靈活適用於多種場景。

缺點

• 需要大量計算資源，尤其是試驗次數多時。
• 結果的準確性依賴於輸入數據的質量和概率分布的假設。
• 對模型的理解和設置要求較高。

總結

蒙特卡羅模擬是一種強大的工具，用於在不確定性下進行決策分析。它通過模擬大量隨機情景，幫助用戶理解可能的結果範圍及其概率，特別適合需要量化風險或不確定性的場景。

以下是一個簡單的教學，展示如何使用蒙特卡羅模擬來估計一個項目的完成時間，並以圖表形式呈現結果。我們將以一個假設的項目為例，包含三個任務，完成時間服從均勻分布，並通過模擬生成總時間的概率分布，最後以直方圖展示結果。

蒙特卡羅模擬圖示教學：估計項目完成時間

情境

假設一個項目有三個任務：

• 任務A：完成時間在5至7天之間（均勻分布）。
• 任務B：完成時間在3至5天之間（均勻分布）。
• 任務C：完成時間在2至4天之間（均勻分布）。

我們將使用蒙特卡羅模擬運行10,000次試驗，計算總完成時間的分布，並以直方圖展示結果。

步驟

1. 定義模型：

• 每個任務的完成時間是隨機的，服從均勻分布。
• 總完成時間 = 任務A時間 + 任務B時間 + 任務C時間。

1. 隨機抽樣：

• 對每個任務，隨機生成一個完成時間：
  • 任務A：隨機數在[5, 7]之間。
  • 任務B：隨機數在[3, 5]之間。
  • 任務C：隨機數在[2, 4]之間。

1. 模擬試驗：

• 重複10,000次，每次生成隨機的任務時間，計算總時間。

1. 分析結果：

• 收集所有試驗的總時間，計算頻率分布。
• 用直方圖展示總時間的概率分布。

模擬結果展示

假設我們運行模擬，得到總完成時間的頻率分布。以下是一個直方圖，顯示總完成時間的分布（假設數據已模擬生成）。

{
  "type": "histogram",
  "data": {
    "labels": ["10", "10.5", "11", "11.5", "12", "12.5", "13", "13.5", "14", "14.5", "15", "15.5", "16"],
    "datasets": [{
      "label": "總完成時間頻率",
      "data": [50, 200, 600, 1200, 2000, 2500, 2200, 1500, 800, 400, 150, 50, 10],
      "backgroundColor": "rgba(54, 162, 235, 0.7)",
      "borderColor": "rgba(54, 162, 235, 1)",
      "borderWidth": 1
    }]
  },
  "options": {
    "scales": {
      "x": {
        "title": {
          "display": true,
          "text": "總完成時間（天）"
        }
      },
      "y": {
        "title": {
          "display": true,
          "text": "頻率"
        }
      }
    },
    "plugins": {
      "title": {
        "display": true,
        "text": "蒙特卡羅模擬：項目完成時間分布"
      }
    }
  }
}

圖表解釋

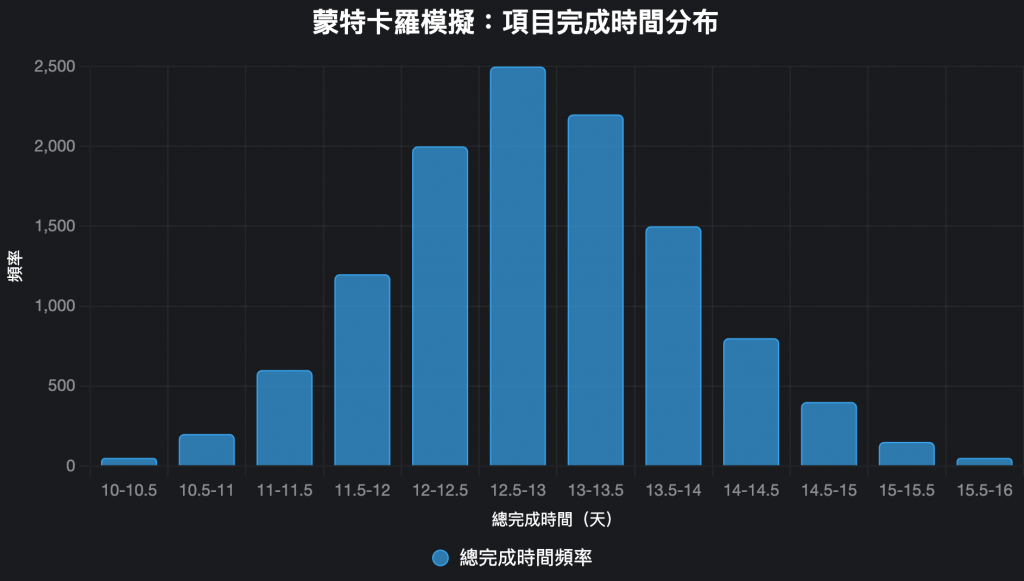
• X軸：表示總完成時間（天），範圍從10天到16天（因為最小值5+3+2=10，最大值7+5+4=16）。
• Y軸：表示該時間範圍的頻率（試驗次數）。
• 分佈形狀：模擬結果顯示總完成時間大多集中在12至14天之間，這表明項目很可能在這個時間範圍內完成。
• 概率分析：
• 可以從圖表推算，例如，90%的試驗結果可能落在11.5至14.5天之間。
• 平均完成時間約為13天（可通過模擬數據計算）。

教學重點

1. 輸入不確定性：每個任務的時間不是固定的，而是隨機的，模擬真實世界的不確定性。
2. 大量試驗：10,000次試驗確保結果的統計可靠性。
3. 視覺化：直方圖清楚展示結果的概率分布，幫助決策者理解風險和可能性。
4. 應用場景：這種方法可用於項目管理、金融風險分析、工程設計等。

如何實現模擬

以下是一個簡單的Python偽代碼，展示如何生成模擬數據（僅供參考，無需執行）：

import numpy as np
import matplotlib.pyplot as plt

# 設置試驗次數
n_trials = 10000
# 隨機抽樣任務時間
task_a = np.random.uniform(5, 7, n_trials)
task_b = np.random.uniform(3, 5, n_trials)
task_c = np.random.uniform(2, 4, n_trials)
# 計算總時間
total_time = task_a + task_b + task_c
# 繪製直方圖
plt.hist(total_time, bins=30, density=True)
plt.xlabel('總完成時間（天）')
plt.ylabel('頻率')
plt.title('蒙特卡羅模擬：項目完成時間分布')
plt.show()

總結

這個教學展示了蒙特卡羅模擬的基本流程：定義問題、隨機抽樣、多次試驗、分析結果，並通過直方圖視覺化結果。這種方法能有效處理不確定性，幫助決策者更好地理解風險和可能性。